numpy.meshgrid#

numpy.meshgrid(*xi, copy=True, sparse=False, indexing='xy')[源代码]#

从坐标向量返回坐标矩阵的元组.

给定一维坐标数组 x1, x2,…, xn,为 N 维标量/向量场在 N 维网格上的向量化评估生成 N 维坐标数组.

参数:
x1, x2,…, xnarray_like

表示网格坐标的 1-D 数组.

indexing{‘xy’, ‘ij’}, 可选

输出的笛卡尔坐标系(‘xy’,默认)或矩阵坐标系(‘ij’). 详见注释.

sparsebool,可选

如果为真,则维度 i 的返回坐标数组的形状从 (N1, ..., Ni, ... Nn) 减少到 (1, ..., 1, Ni, 1, ..., 1) . 这些稀疏坐标网格旨在与 广播 一起使用. 当表达式中使用所有坐标时,广播仍然会产生一个完全维度的结果数组.

默认为 False.

copybool,可选

如果为假,为了节省内存,会返回原始数组的视图.默认为 True. 请注意, sparse=False, copy=False 可能会返回非连续数组. 此外,广播数组的多个元素可能指向同一个内存位置. 如果需要写入数组,请先复制.

返回:
X1, X2,…, XNndarray 元组

对于长度为 Ni=len(xi) 的向量 x1 , x2 ,…, xn ,如果 indexing=’ij’,则返回形状为 (N1, N2, N3,..., Nn) 的数组;如果 indexing=’xy’,则返回形状为 (N2, N1, N3,..., Nn) 的数组,其中 xi 的元素被重复以沿第一个维度填充矩阵(对于 x1 ),沿第二个维度填充矩阵(对于 x2 ),依此类推.

参见

mgrid

使用索引符号构造一个多维"meshgrid".

ogrid

使用索引符号构造一个开放的多维"meshgrid".

如何索引 ndarrays

注释

此函数通过 indexing 关键字参数支持这两种索引约定. 给定字符串"ij"返回一个具有矩阵索引的 meshgrid,而"xy"返回一个具有笛卡尔索引的 meshgrid. 在长度为 M 和 N 的 2-D 情况下,对于"xy"索引,输出的形状为 (N, M),对于"ij"索引,输出的形状为 (M, N). 在长度为 M,N 和 P 的 3-D 情况下,对于"xy"索引,输出的形状为 (N, M, P),对于"ij"索引,输出的形状为 (M, N, P). 以下代码片段说明了差异:

xv, yv = np.meshgrid(x, y, indexing='ij')
for i in range(nx):
    for j in range(ny):
        # treat xv[i,j], yv[i,j]

xv, yv = np.meshgrid(x, y, indexing='xy')
for i in range(nx):
    for j in range(ny):
        # treat xv[j,i], yv[j,i]

在一维和零维情况下,索引和稀疏关键字不起作用.

示例

>>> import numpy as np
>>> nx, ny = (3, 2)
>>> x = np.linspace(0, 1, nx)
>>> y = np.linspace(0, 1, ny)
>>> xv, yv = np.meshgrid(x, y)
>>> xv
array([[0. , 0.5, 1. ],
       [0. , 0.5, 1. ]])
>>> yv
array([[0.,  0.,  0.],
       [1.,  1.,  1.]])

meshgrid 的结果是一个坐标网格:

>>> import matplotlib.pyplot as plt
>>> plt.plot(xv, yv, marker='o', color='k', linestyle='none')
>>> plt.show()
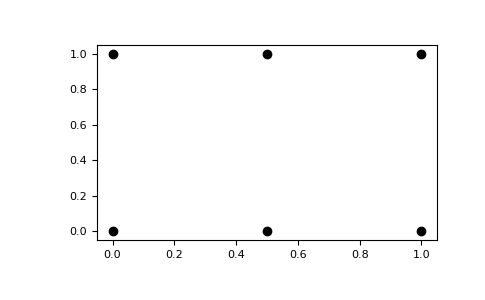
../../_images/numpy-meshgrid-1_00_00.png

您可以创建稀疏输出数组以节省内存和计算时间.

>>> xv, yv = np.meshgrid(x, y, sparse=True)
>>> xv
array([[0. ,  0.5,  1. ]])
>>> yv
array([[0.],
       [1.]])

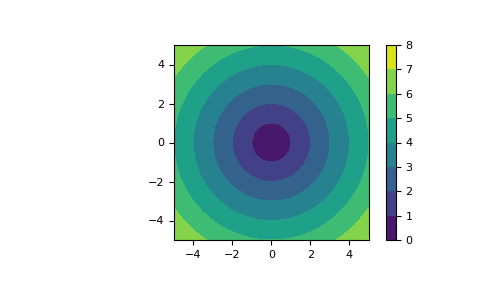
meshgrid 对于在网格上评估函数非常有用.如果函数依赖于所有坐标,则可以使用密集和稀疏输出.

>>> x = np.linspace(-5, 5, 101)
>>> y = np.linspace(-5, 5, 101)
>>> # full coordinate arrays
>>> xx, yy = np.meshgrid(x, y)
>>> zz = np.sqrt(xx**2 + yy**2)
>>> xx.shape, yy.shape, zz.shape
((101, 101), (101, 101), (101, 101))
>>> # sparse coordinate arrays
>>> xs, ys = np.meshgrid(x, y, sparse=True)
>>> zs = np.sqrt(xs**2 + ys**2)
>>> xs.shape, ys.shape, zs.shape
((1, 101), (101, 1), (101, 101))
>>> np.array_equal(zz, zs)
True

>>> h = plt.contourf(x, y, zs)
>>> plt.axis('scaled')
>>> plt.colorbar()
>>> plt.show()
../../_images/numpy-meshgrid-1_01_00.png
On this page