numpy.random.noncentral_chisquare

random.noncentral_chisquare(df, nonc, size=None)

从非中心卡方分布中抽取样本.

非中心 \(\chi^2\) 分布是 \(\chi^2\) 分布的推广.

备注

新代码应该使用 noncentral_chisquare 方法,该方法属于 Generator 实例;请参考 快速入门 .

参数:

dffloat 或 float 的类数组

自由度,必须 > 0.

noncfloat 或 float 的类数组

非中心性,必须是非负的.

sizeint 或 int 元组,可选

输出形状.如果给定的形状是,例如 (m, n, k) ,则抽取 m * n * k 个样本.如果 size 是 None (默认),则如果 df 和 nonc 都是标量,则返回单个值.否则,抽取 np.broadcast(df, nonc).size 个样本.

返回:

outndarray 或标量

从参数化的非中心卡方分布中抽取的样本.

参见

random.Generator.noncentral_chisquare

新代码应该使用它.

注释

非中心卡方分布的概率密度函数为

\[P(x;df,nonc) = \sum^{\infty}_{i=0} \frac{e^{-nonc/2}(nonc/2)^{i}}{i!} P_{Y_{df+2i}}(x),\]

其中 \(Y_{q}\) 是具有 q 个自由度的卡方分布.

参考文献

[1]

Wikipedia, “Noncentral chi-squared distribution” https://en.wikipedia.org/wiki/Noncentral_chi-squared_distribution

示例

Try it in your browser!

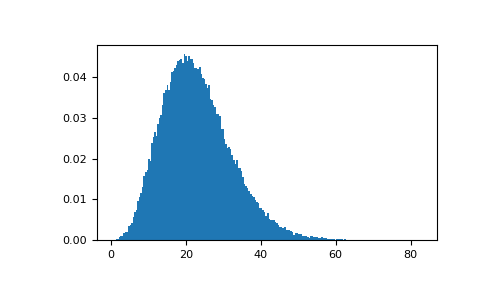
从分布中绘制值并绘制直方图

>>> import matplotlib.pyplot as plt
>>> values = plt.hist(np.random.noncentral_chisquare(3, 20, 100000),
...                   bins=200, density=True)
>>> plt.show()

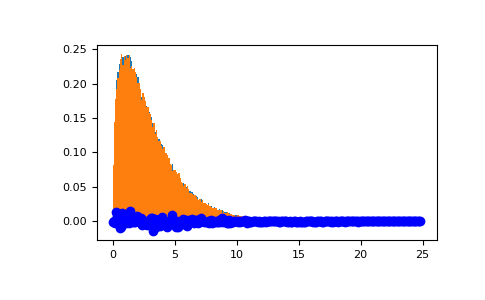
从具有非常小的非中心性的非中心卡方中绘制值,并与卡方进行比较.

>>> plt.figure()
>>> values = plt.hist(np.random.noncentral_chisquare(3, .0000001, 100000),
...                   bins=np.arange(0., 25, .1), density=True)
>>> values2 = plt.hist(np.random.chisquare(3, 100000),
...                    bins=np.arange(0., 25, .1), density=True)
>>> plt.plot(values[1][0:-1], values[0]-values2[0], 'ob')
>>> plt.show()

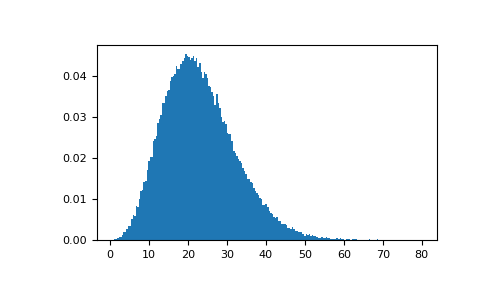
演示非中心性的较大值如何导致更对称的分布.

>>> plt.figure()
>>> values = plt.hist(np.random.noncentral_chisquare(3, 20, 100000),
...                   bins=200, density=True)
>>> plt.show()

Go BackOpen In Tab