numpy.random.Generator.binomial#
method
- random.Generator.binomial(n, p, size=None)#
从二项分布中抽取样本.
样本是从具有指定参数的二项分布中抽取的,n 次试验和 p 成功概率,其中 n 是 >= 0 的整数,p 在区间 [0,1] 中.(n 可以作为浮点数输入,但在使用时会被截断为整数)
- 参数:
- nint 或 int 的类数组
分布的参数,>= 0.也接受浮点数,但它们将被截断为整数.
- pfloat 或 float 的类数组
分布的参数,>= 0 且 <=1.
- sizeint 或 int 元组,可选
输出形状.例如,如果给定的形状是
(m, n, k),则抽取m * n * k个样本.如果 size 是None(默认值),则当n和p都是标量时,返回单个值.否则,抽取np.broadcast(n, p).size个样本.
- 返回:
- outndarray 或标量
从参数化的二项分布中抽取的样本,其中每个样本等于 n 次试验中成功的次数.
参见
scipy.stats.binom概率密度函数,分布或累积密度函数等.
注释
二项分布的概率质量函数 (PMF) 为
\[P(N) = \binom{n}{N}p^N(1-p)^{n-N},\]其中 \(n\) 是试验次数, \(p\) 是成功的概率, \(N\) 是成功的次数.
当使用随机样本估计总体中比例的标准误差时,正态分布效果很好,除非乘积 pn <=5,其中 p = 总体比例估计,n = 样本数,在这种情况下,应使用二项分布.例如,一个由 15 人组成的样本显示 4 人是左撇子,11 人是右撇子.那么 p = 4/15 = 27%.0.2715 = 4,因此在这种情况下应使用二项分布.
参考文献
[1]Dalgaard, Peter, “Introductory Statistics with R”, Springer-Verlag, 2002.
[2]Glantz, Stanton A. “Primer of Biostatistics.”, McGraw-Hill, Fifth Edition, 2002.
[3]Lentner, Marvin, “Elementary Applied Statistics”, Bogden and Quigley, 1972.
[4]Weisstein, Eric W. “Binomial Distribution.” From MathWorld–A Wolfram Web Resource. https://mathworld.wolfram.com/BinomialDistribution.html
[5]Wikipedia, “Binomial distribution”, https://en.wikipedia.org/wiki/Binomial_distribution
示例
从分布中抽取样本:
>>> rng = np.random.default_rng() >>> n, p, size = 10, .5, 10000 >>> s = rng.binomial(n, p, 10000)
假设一家公司钻探了 9 口野猫油气勘探井,每口井的估计成功概率为
p=0.1.所有九口井都失败了.发生这种情况的概率是多少?在
size = 20,000次试验中,发生这种情况的平均概率为:>>> n, p, size = 9, 0.1, 20000 >>> np.sum(rng.binomial(n=n, p=p, size=size) == 0)/size 0.39015 # may vary
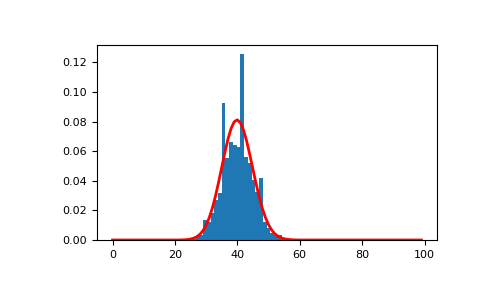
以下代码可用于可视化一个样本,其中
n=100,p=0.4以及相应的概率密度函数:>>> import matplotlib.pyplot as plt >>> from scipy.stats import binom >>> n, p, size = 100, 0.4, 10000 >>> sample = rng.binomial(n, p, size=size) >>> count, bins, _ = plt.hist(sample, 30, density=True) >>> x = np.arange(n) >>> y = binom.pmf(x, n, p) >>> plt.plot(x, y, linewidth=2, color='r')