numpy.random.Generator.weibull#
method
- random.Generator.weibull(a, size=None)#
从 Weibull 分布中抽取样本.
从具有给定形状参数 a 的单参数 Weibull 分布中抽取样本.
\[X = (-ln(U))^{1/a}\]这里,U 是从 (0,1] 上的均匀分布中抽取的.
更常见的双参数 Weibull 分布,包括比例参数 \(\lambda\) 只是 \(X = \lambda(-ln(U))^{1/a}\) .
- 参数:
- afloat 或 floats 的类数组对象
分布的形状参数.必须是非负数.
- sizeint 或 int 的元组,可选.
输出形状.如果给定的形状是例如
(m, n, k),则抽取m * n * k个样本.如果 size 为None(默认值),则如果a是标量,则返回单个值.否则,抽取np.array(a).size个样本.
- 返回:
- outndarray 或标量
从参数化的 Weibull 分布中抽取的样本.
注释
Weibull 分布(或最小值的 III 型渐近极值分布,SEV Type III,或 Rosin-Rammler 分布)是用于对极值问题进行建模的广义极值(GEV)分布类别之一.此类包括 Gumbel 分布和 Frechet 分布.
Weibull 分布的概率密度为
\[p(x) = \frac{a} {\lambda}(\frac{x}{\lambda})^{a-1}e^{-(x/\lambda)^a},\]其中 \(a\) 是形状, \(\lambda\) 是比例.
该函数在 \(\lambda(\frac{a-1}{a})^{1/a}\) 处达到峰值(众数).
当
a = 1时,Weibull 分布简化为指数分布.参考
[1]Waloddi Weibull, Royal Technical University, Stockholm, 1939 “A Statistical Theory Of The Strength Of Materials”, Ingeniorsvetenskapsakademiens Handlingar Nr 151, 1939, Generalstabens Litografiska Anstalts Forlag, Stockholm.
[2]Waloddi Weibull, “A Statistical Distribution Function of Wide Applicability”, Journal Of Applied Mechanics ASME Paper 1951.
[3]Wikipedia, “Weibull distribution”, https://en.wikipedia.org/wiki/Weibull_distribution
示例
从分布中抽取样本:
>>> rng = np.random.default_rng() >>> a = 5. # shape >>> s = rng.weibull(a, 1000)
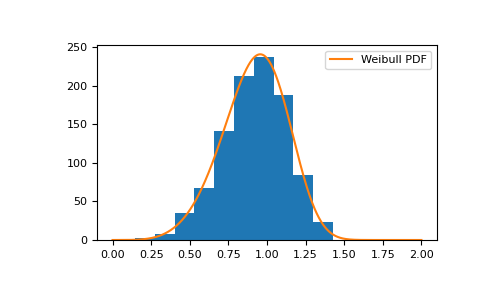
显示样本的直方图,以及概率密度函数:
>>> import matplotlib.pyplot as plt >>> def weibull(x, n, a): ... return (a / n) * (x / n)**(a - 1) * np.exp(-(x / n)**a) >>> count, bins, _ = plt.hist(rng.weibull(5., 1000)) >>> x = np.linspace(0, 2, 1000) >>> bin_spacing = np.mean(np.diff(bins)) >>> plt.plot(x, weibull(x, 1., 5.) * bin_spacing * s.size, label='Weibull PDF') >>> plt.legend() >>> plt.show()
