numpy.random.Generator.standard_cauchy#
method
- random.Generator.standard_cauchy(size=None)#
从 mode = 0 的标准柯西分布中抽取样本.
也称为洛伦兹分布.
- 参数:
- sizeint 或 int 的元组,可选.
输出形状.如果给定的形状是,例如
(m, n, k),则抽取m * n * k个样本.默认值为 None,在这种情况下,将返回单个值.
- 返回:
- 样本ndarray 或标量
绘制的样本.
注释
完整柯西分布的概率密度函数为
\[P(x; x_0, \gamma) = \frac{1}{\pi \gamma \bigl[ 1+ (\frac{x-x_0}{\gamma})^2 \bigr] }\]标准柯西分布仅设置 \(x_0=0\) 和 \(\gamma=1\)
柯西分布出现在驱动谐振子问题的解中,并且也描述了谱线加宽.它还描述了以随机角度倾斜的线将切割 x 轴的值的分布.
当研究假设正态性的假设检验时,查看检验在来自柯西分布的数据上的表现如何,可以很好地指示它们对重尾分布的敏感性,因为柯西看起来非常像高斯分布,但具有更重的尾部.
参考
[1]NIST/SEMATECH e-Handbook of Statistical Methods, “Cauchy Distribution”, https://www.itl.nist.gov/div898/handbook/eda/section3/eda3663.htm
[2]Weisstein, Eric W. “Cauchy Distribution.” From MathWorld–A Wolfram Web Resource. https://mathworld.wolfram.com/CauchyDistribution.html
[3]Wikipedia, “Cauchy distribution” https://en.wikipedia.org/wiki/Cauchy_distribution
示例
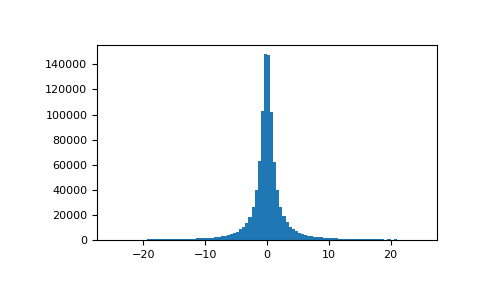
绘制样本并绘制分布图:
>>> import matplotlib.pyplot as plt >>> rng = np.random.default_rng() >>> s = rng.standard_cauchy(1000000) >>> s = s[(s>-25) & (s<25)] # truncate distribution so it plots well >>> plt.hist(s, bins=100) >>> plt.show()
