numpy.random.Generator.exponential#
method
- random.Generator.exponential(scale=1.0, size=None)#
从指数分布中抽取样本.
其概率密度函数为
\[f(x; \frac{1}{\beta}) = \frac{1}{\beta} \exp(-\frac{x}{\beta}),\]对于
x > 0,其他地方为 0. \(\beta\) 是尺度参数,它是速率参数 \(\lambda = 1/\beta\) 的倒数.速率参数是指数分布的另一种广泛使用的参数化方法 [3].指数分布是几何分布的连续模拟.它描述了许多常见情况,例如多次暴雨中测量的雨滴大小 [1],或对维基百科的页面请求之间的时间 [2] .
- 参数:
- scalefloat 或 floats 的类数组对象
尺度参数, \(\beta = 1/\lambda\) .必须是非负数.
- sizeint 或 int 的元组,可选.
输出形状.如果给定的形状是,例如,
(m, n, k),则抽取m * n * k个样本.如果 size 为None(默认值),则如果scale是标量,则返回单个值.否则,抽取np.array(scale).size个样本.
- 返回:
- outndarray 或标量
从参数化的指数分布中抽取样本.
参考
[1]Peyton Z. Peebles Jr., “Probability, Random Variables and Random Signal Principles”, 4th ed, 2001, p. 57.
[2]Wikipedia, “Poisson process”, https://en.wikipedia.org/wiki/Poisson_process
[3]Wikipedia, “Exponential distribution”, https://en.wikipedia.org/wiki/Exponential_distribution
示例
假设一家公司有 10000 名客户支持代理,并且客户呼叫之间的时间呈指数分布,并且客户呼叫之间的平均时间为 4 分钟.
>>> scale, size = 4, 10000 >>> rng = np.random.default_rng() >>> time_between_calls = rng.exponential(scale=scale, size=size)
客户在未来 4 到 5 分钟内呼叫的概率是多少?
>>> x = ((time_between_calls < 5).sum())/size >>> y = ((time_between_calls < 4).sum())/size >>> x - y 0.08 # may vary
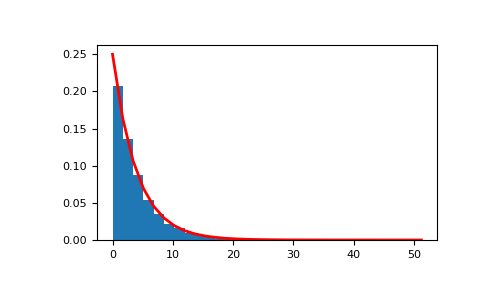
相应的分布可以可视化如下:
>>> import matplotlib.pyplot as plt >>> scale, size = 4, 10000 >>> rng = np.random.default_rng() >>> sample = rng.exponential(scale=scale, size=size) >>> count, bins, _ = plt.hist(sample, 30, density=True) >>> plt.plot(bins, scale**(-1)*np.exp(-scale**-1*bins), linewidth=2, color='r') >>> plt.show()
