numpy.exp#
- numpy.exp(x, /, out=None, *, where=True, casting='same_kind', order='K', dtype=None, subok=True[, signature]) = <ufunc 'exp'>#
计算输入数组中所有元素的指数.
- 参数:
- xarray_like
输入值.
- outndarray, None, or tuple of ndarray and None, optional
存储结果的位置.如果提供,则它必须具有输入广播到的形状.如果未提供或为None,则返回一个新分配的数组.一个元组(可能仅作为关键字参数)的长度必须等于输出的数量.
- 其中类数组,可选
此条件会在输入上进行广播.在条件为True的位置, out 数组将被设置为ufunc结果.否则, out 数组将保留其原始值.请注意,如果通过默认的
out=None创建一个未初始化的 out 数组,则其中条件为False的位置将保持未初始化.- \kwargs
对于其他仅限关键字的参数,请参见 ufunc docs .
- 返回:
- outndarray 或标量
输出数组, x 的逐元素指数.如果 x 是标量,则这是一个标量.
注释
无理数
e也被称为欧拉数.它近似等于 2.718281,是自然对数的底数,ln(这意味着,如果 \(x = \ln y = \log_e y\) ,那么 \(e^x = y\) .对于实数输入,exp(x)始终为正数.)对于复数参数,
x = a + ib,我们可以写成 \(e^x = e^a e^{ib}\) .第一项, \(e^a\) ,是已知的(它是实数参数,如上所述).第二项, \(e^{ib}\) ,是 \(\cos b + i \sin b\) ,一个幅度为 1 且具有周期性相位的函数.参考文献
[1]维基百科,"指数函数",https://en.wikipedia.org/wiki/Exponential_function
[2]M. Abramovitz and I. A. Stegun, “Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables,” Dover, 1964, p. 69, https://personal.math.ubc.ca/~cbm/aands/page_69.htm
示例
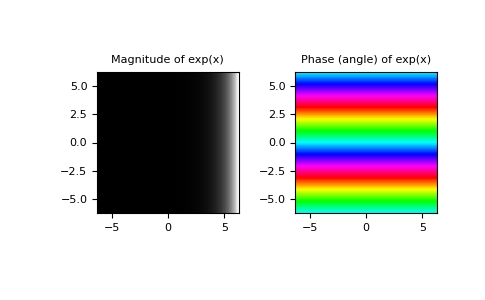
在复平面上绘制
exp(x)的幅度和相位:>>> import numpy as np
>>> import matplotlib.pyplot as plt >>> import numpy as np
>>> x = np.linspace(-2*np.pi, 2*np.pi, 100) >>> xx = x + 1j * x[:, np.newaxis] # a + ib over complex plane >>> out = np.exp(xx)
>>> plt.subplot(121) >>> plt.imshow(np.abs(out), ... extent=[-2*np.pi, 2*np.pi, -2*np.pi, 2*np.pi], cmap='gray') >>> plt.title('Magnitude of exp(x)')
>>> plt.subplot(122) >>> plt.imshow(np.angle(out), ... extent=[-2*np.pi, 2*np.pi, -2*np.pi, 2*np.pi], cmap='hsv') >>> plt.title('Phase (angle) of exp(x)') >>> plt.show()