numpy.interp#
- numpy.interp(x, xp, fp, left=None, right=None, period=None)[源代码]#
单调递增采样点的一维线性插值.
返回给定离散数据点 ( xp , fp ) 函数的一维分段线性插值,并在 x 处求值.
- 参数:
- xarray_like
在这些x坐标处求插值.
- xp浮点数的一维序列
数据点的x坐标,如果未指定参数 period ,则必须递增.否则,在利用
xp = xp % period归一化周期边界后,将在内部对 xp 进行排序.- fp浮点数或复数的一维序列
数据点的y坐标,与 xp 的长度相同.
- left对应于 fp 的可选浮点数或复数
当 x < xp[0] 时返回的值,默认为 fp[0] .
- right对应于 fp 的可选浮点数或复数
当 x > xp[-1] 时返回的值,默认为 fp[-1] .
- periodNone 或 float,可选
x坐标的周期.此参数允许对角度x坐标进行适当的插值.如果指定了 period ,则忽略参数 left 和 right .
- 返回:
- yfloat 或 complex (对应于 fp) 或 ndarray
插值,与 x 的形状相同.
- Raises:
- ValueError
如果 xp 和 fp 的长度不同 如果 xp 或 fp 不是一维序列 如果 period == 0
警告
x坐标序列应为递增序列,但这并非强制执行.但是,如果序列 xp 不递增,则插值结果将毫无意义.
请注意,由于 NaN 是不可排序的,因此 xp 也不能包含 NaN.
一个简单的检查 xp 是否严格递增的方法是:
np.all(np.diff(xp) > 0)
示例
>>> import numpy as np >>> xp = [1, 2, 3] >>> fp = [3, 2, 0] >>> np.interp(2.5, xp, fp) 1.0 >>> np.interp([0, 1, 1.5, 2.72, 3.14], xp, fp) array([3. , 3. , 2.5 , 0.56, 0. ]) >>> UNDEF = -99.0 >>> np.interp(3.14, xp, fp, right=UNDEF) -99.0
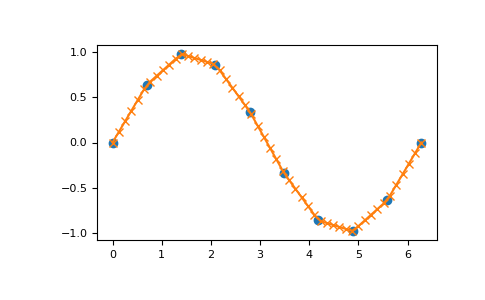
绘制正弦函数的插值:
>>> x = np.linspace(0, 2*np.pi, 10) >>> y = np.sin(x) >>> xvals = np.linspace(0, 2*np.pi, 50) >>> yinterp = np.interp(xvals, x, y) >>> import matplotlib.pyplot as plt >>> plt.plot(x, y, 'o') [<matplotlib.lines.Line2D object at 0x...>] >>> plt.plot(xvals, yinterp, '-x') [<matplotlib.lines.Line2D object at 0x...>] >>> plt.show()
使用周期性x坐标进行插值:
>>> x = [-180, -170, -185, 185, -10, -5, 0, 365] >>> xp = [190, -190, 350, -350] >>> fp = [5, 10, 3, 4] >>> np.interp(x, xp, fp, period=360) array([7.5 , 5. , 8.75, 6.25, 3. , 3.25, 3.5 , 3.75])
复数插值:
>>> x = [1.5, 4.0] >>> xp = [2,3,5] >>> fp = [1.0j, 0, 2+3j] >>> np.interp(x, xp, fp) array([0.+1.j , 1.+1.5j])